
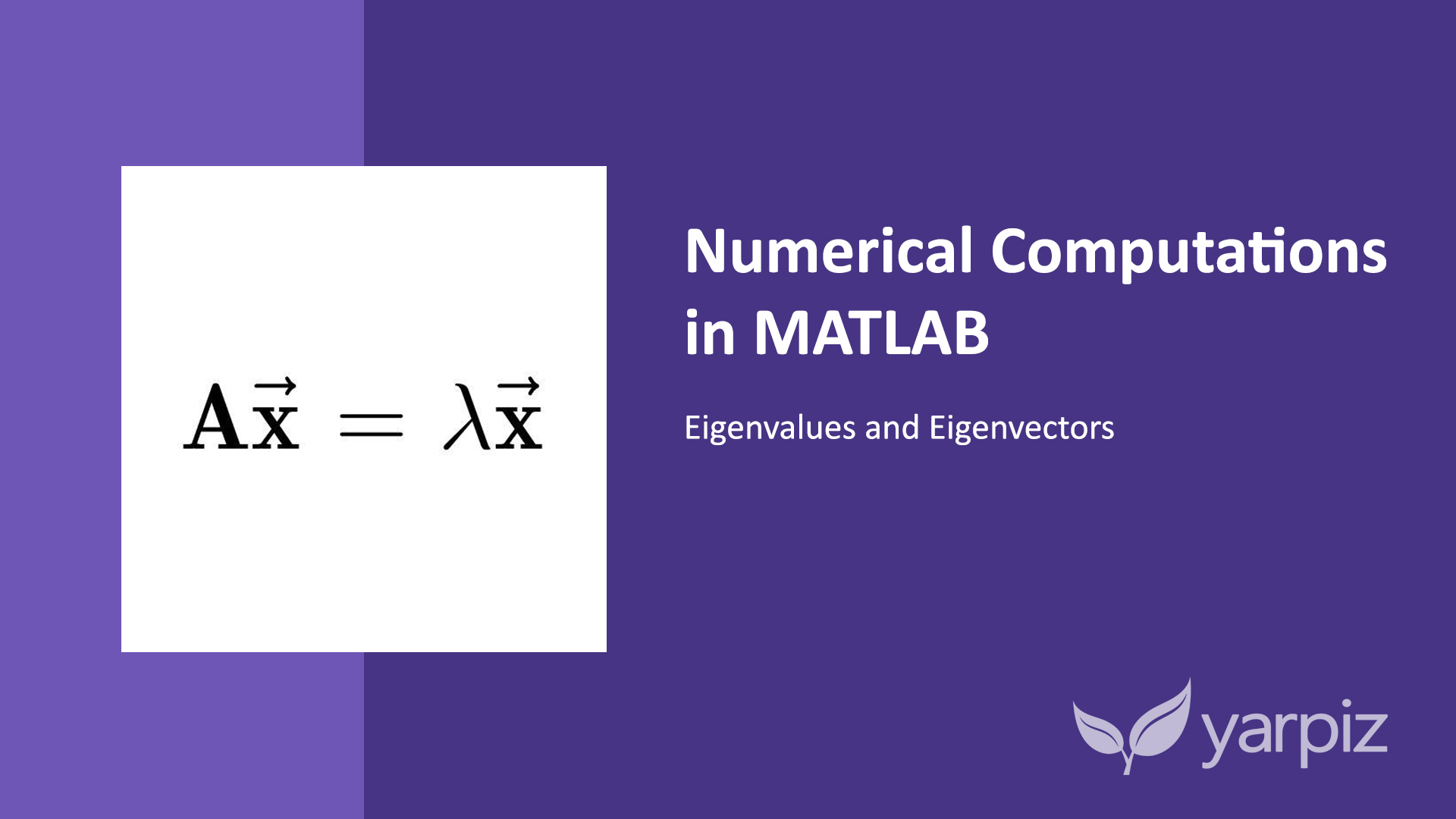
The algorithms related to solving a linear system of equations are also described there.
GET EIGENVALUES MATLAB CODE
To find the eigenvectors is a matter of solving two linear systems of equations of the form \(A * x = b\):įrom a code perspective, if you want to do it in C, you take a look at my “academical” called nml.

We define two matrices \(A\) and \(B\) as being similar if there exists a non-singular matrix \(X\) such that: \(B=X^=1\). A matrix \(A\) can be decomposed like: \(A = Q * R\), where \(R\) is an upper triangular matrix, and Q is an orthonormal matrix.īecause \(Q\) is orthonormal, it has a few unique properties:įrom a computational perspective, this leads to some advantages because the inverse of an orthonormal matrix is the same as its transpose. In case you haven’t done so, I recommend you to read the linked sub-chapters first, as it will be easier to follow through.Įven if it’s not very obvious, the QR Decomposition (\(A = Q * R\)) of a matrix \(A\) is useful to compute the eigenvalues/eigenvectors associated with \(A\).īut, let’s recap. In my last two articles, I’ve tried to explore some fundamental topics in linear algebra: QR Decomposition, linear transformations and Eigenvalues/Eigenvectors. Consider yourself lucky if you have 2 significative digits.Computing Eigenvalues and Eigenvectors using QR Decomposition If you wish to verify this experimentally, I guess you'll have a hard time getting an exact zero out of Matlab, since this sum converges quite slowly to its asymptotical value usually. If another eigenvector were to be nonnegative, then the scalar product with the dominant eigenvector $u^^n (\phi_t-\mu) (\phi'_t-\mu)'^T=0$, where $\mu$ and $\mu'$ are the means of the two time series. There are some classes of matrices (such as Z-matrices or nonnegative matrices) for which it is known that the largest or smallest eigenvector is nonnegative. This not only computes the eigenvalues and eigenvectors for you, but it will compute the k largest eigenvalues with their associated eigenvectors for you. What I would recommend to you in the future is to use the eigs function. No, the eigenvalues could come in any order there is no guarantee that they are ordered. 1 Answer Sorted by: 24 I'm assuming you determined the eigenvectors from the eig function. I suppose your matrix is symmetric, since you say that the eigenvectors are orthogonal and try to order the eigenvalues.

LOTS of questions, I know, but I would REALLY appreciate if you could help me answer some of them!
GET EIGENVALUES MATLAB HOW TO
Out of curiosity, but what does it mean "the two times-series Fi and Fi' are uncorrelated in the sense that their empirical correlation vanishes for i != i' ? How to check that in MATLAB?.

Actually, I want eigenvalues and their corresponding eigenectors in decreasing order, and then select the, 2 say, "most significant" ones.Do eigenvalues-eigenvectors come in pairs? If yes, and considering the above, then does the corresponding eigenvalue lay on the bottom-right of matrix D?.Regarding the "corresponding eigenvecrtors", do we read them "column-by-column" OR "row-by-row"?.Every eigenvalue corresponds to an eigenvector. Then the values X, satisfying the equation are eigenvectors and eigenvalues of matrix A respectively.
Let is an NN matrix, X be a vector of size N1 and be a scalar. Using QR decomposition to determine the eigenvalues and eigenvectors of a matrix The algorithm in its most basic form looks like this: for (Q, R) decomposeqr (A) A R Q Eventually, under desired conditions, A A will converge to the Schur Form of A A (which is U U from the formula A Q U Q1 A Q U Q 1 ).

 0 kommentar(er)
0 kommentar(er)
